![]() Difficulté : pas de problématiques particulière
Difficulté : pas de problématiques particulière
![]() Utilisateurs : enseignants 1er et 2nd degrés
Utilisateurs : enseignants 1er et 2nd degrés
![]() Niveau scolaire : collège – lycée
Niveau scolaire : collège – lycée
Présentation et intérêt pédagogique
Les représentations graphiques de certaines données ou statistiques sont un format particulier d'images qui peuvent transmettre des informations de manière orientée, au mieux de manière involontaire, à cause d'une erreur dans la construction du schéma, au pire de manière volontaire, dans un but manifeste de présenter l'information selon un point de vue idéologique précis.
C'est un grand classique de la communication politique et de certains médias où l'on présente des chiffres et graphiques de manière orientée, de telle façon qu'ils soutiennent un discours et des idées, par opposition à la communication scientifique où (en principe…) on présente les données brutes dans une représentation graphique neutre et mathématiquement juste.
Exemple d'utilisation⚓
Une graphique est construit pour visualiser une importante quantité de données, si possible de la manière la plus synthétique, la plus simple possible. Il est cependant facile pour l'auteur du graphique de se tromper lors de sa construction en faisant des mauvais choix de mise en forme pour la visualisation des données dans son graphique. Ces mauvais choix peuvent être simplement involontaires, par manque d'expérience ou de connaissances, ou au contraire être fait sciemment, par volonté de tromper le lecteur.
On peut remarques plusieurs types d'erreurs (ou plusieurs stratégies trompeuses) :
Représentation visuelle non conforme aux valeurs affichées
Variations incohérentes au sein d'un même schéma
Erreur mathématique dans la construction
Omission de données
Construction incomplète (axes tronqués, disparition des axes et des échelles)
Exemple :
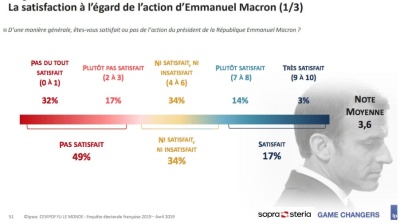
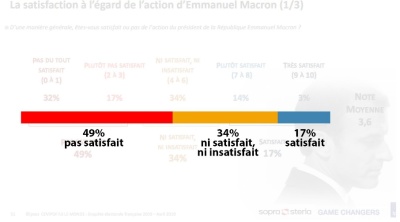
Exemple ci-dessous à gauche d'une représentation graphique totalement erronée, trompeuse, par l'utilisation de dimensions complètement fantaisistes pour l'axe coloré, où on s'aperçoit qu'on a exactement la même longueur d'axe pour matérialiser les 49 % à gauche de l'image et les 17 % à droite de l'image.
À droite, le même axe coloré tel qu'il aurait dû être représenté.
Ces deux images sont extraites de l'excellente conférence « Comment mentir avec des graphiques – Les dessous de nos médias », de Christophe Bontemps :
Site internet : http://data.visualisation.free.fr/
Une vidéo de cette conférence est disponible : https://vimeo.com/381895600
Comment faire⚓
Attention :
L'image est un moyen de communication puissant grâce à sa capacité à générer de l'émotion.
L'objectif initial de simplement transmettre ou renforcer une information est largement dépassé avec le potentiel émotionnel dû à l'image elle-même : l'efficacité de ce média est très forte, une image est très attractive dans un contenu et peut avoir un grand pouvoir de conviction.
Logiquement, l'image est très utilisée pour manipuler les lecteurs ou les spectateurs qui la voient, qui la regardent, car l'émotion qu'elle peut générer est indispensable ou inévitable dans le processus de prise de décision (marketing, design, communication, propagande, etc.)
Les représentations graphiques de données n'échappent pas à la manipulation, toute la difficulté étant d'arriver à prouver si elle est volontaire ou pas.
Exemple : Représentation visuelle non conforme aux valeurs affichées
Ce premier type d'erreurs est très largement répandu. Les grands médias d'information n'y échappent pas.
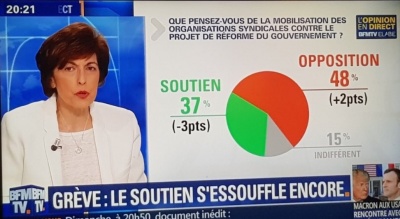
La partie rouge du schéma, sensée représenter la part de la population opposée à la grève, couvre une surface supérieure à la moitié du disque, donc supérieure à 50 %, alors que la valeur est en réalité de 48 %.
Simple erreur dans la conception ou volonté délibérée d'exagérer l'impact du graphique en grossissant artificiellement la partie rouge représentant les personnes opposée à la grève… ?
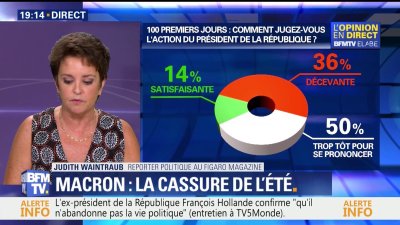
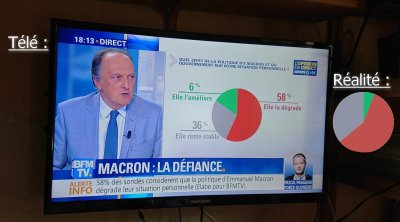
Même principe sur le graphique ci-contre, avec une erreur encore plus grosse : la proportion de personnes qui « jugent décevante l'action du président de la République » est de 36 % et pourtant elle est représentée par une zone qui couvre la moitié du disque, donc 50 %.
Troisième graphique issu lui aussi, comme les deux premiers, de la chaîne d'info en continu BFMTV. Sur la droite de l'image a été rajouté le schéma tel qu'il aurait dû être présenté pour être mathématiquement correct. Au lieu de ça, la partie verte représentant la proportion de personnes favorables à la politique du Président (6 %) a été artificiellement élargie au détriment des deux autres parties. Erreur ou manipulation ?
Où l'on commence à se demander s'il ne faudrait pas que BFMTV paye des cours de maths à ses infographistes…
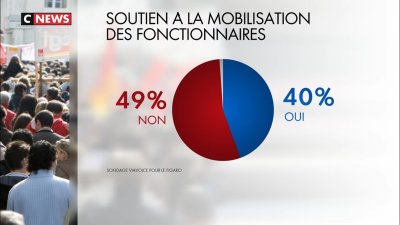
Passons à CNews, chez qui les 49 % de personnes qui soutiennent la mobilisation des fonctionnaires sont représentés par une zone largement supérieure à la moitié du disque sur le schéma ci-contre, donc largement supérieur à 50 %…
La question est : comment peut-on laisser passer une erreur aussi grossière et publier un schéma faux comme celui-ci ?
Bien évidemment, le pas sera vite franchi pour dire qu'il s'agit là d'une volonté délibérée d'influencer l'opinion par l'impact visuel du graphique dont on perçoit au premier coup d'œil qu'une large majorité des personnes ne soutient pas la mobilisation des fonctionnaires.
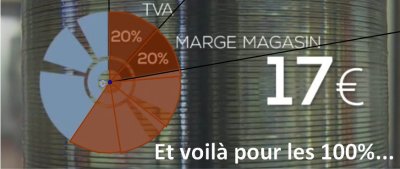
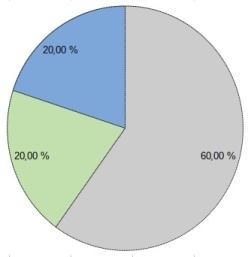
Un autre graphique faux où la part de la TVA et celle de la marge du magasin par rapport au prix de vente d'un DVD sont minimisées. Si ces parts représentent 20 % chacune, soit 40 % en tout, c'est à dire un peu moins de la moitié, elles devraient représenter logiquement un peu moins de la moitié de la surface du disque utilisé pour cette représentation, ce qui est loin d'être le cas sur cette première image où ces deux parts ne représentant visiblement même pas un quart de ce disque…
Le schéma, tel qu'il devrait être :
Exemple : Confondre taille et surface
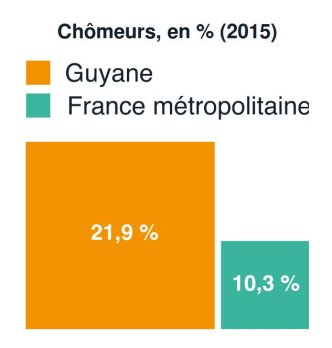
Autre exemple avec cette représentation graphique d'un genre particulier puisqu'elle peut faire tout d'abord penser à un histogramme (où les valeurs sont matérialisées par des « barres » plus ou moins hautes) alors que ça n'en est pas un et que la visualisation est matérialisée par des surfaces :
Dans ces conditions, on ne doit pas représenter la valeur 21,9 % par une zone colorée environ deux fois plus haute que celle pour la valeur 10,3 % si les deux zones colorées n'ont pas la même largeur (comme on l'aurait fait avec un histogramme, avec des « barres » de largeur égale).
Avec le choix de ce graphique, où la visualisation se fait avec des surfaces carrées, on représente donc une valeur double (21,9 %) par une surface (orange) QUATRE fois plus grande que celle de la valeur 10,3 %.
Ce graphique est issu d'un article sur Le Monde, article qui présente de nombreux autres types de graphiques :
Il s'agit manifestement d'une erreur dans le choix de la visualisation de ces données, erreur qui aboutit à une perception faussée des deux grandeurs présentées.
Exemple : Variations incohérentes au sein d'un même schéma
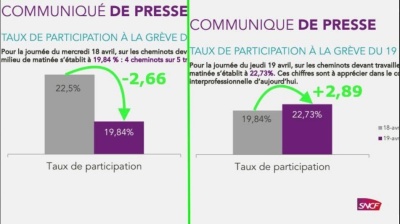
Pour illustrer ce type de graphiques faux, un exemple célèbre qui date des grèves au sein de la SNCF en 2018 : la Direction de la SNCF communiquait quotidiennement sur les taux de grévistes et montrait, d'un jour à l'autre, les variations du taux de grévistes sur des graphiques comme les deux ci-dessous.
Sur ces deux graphiques, publiés à 24 h d'écart les 18 et 19/04/2018, on visualise parfaitement le parti pris qui a été adopté par la Direction de la SNCF pour tenter d'augmenter l'importance d'une variation à la baisse du taux de grévistes (pour le 1er schéma) et de minimiser l'importance d'une variation à la hausse (pour le 2e schéma). Sur le 2e graphique, une hausse de 2,89 % est représentée par un écart qui est visuellement 6 fois plus petit que celui qui représente une baisse de 2,6 % dans le 1er graphique…
➜ on n'est clairement plus dans le domaine de l'information par la présentation neutre de données chiffrées, mais bel et bien dans la communication politique soutenue par la manipulation tendancieuse de graphiques.
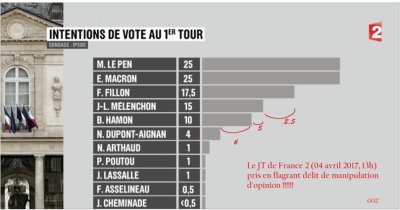
Autre exemple avec ce sondage IPSOS d'avril 2017, en pleine campagne électorale pour le premier tour de l'élection présidentielle.
On observe dans le graphique proposé des écarts (visuels) incohérents, du même type que dans l'exemple précédent, entre les différentes barres des candidats dans l'histogramme : l'écart de 2,5 % entre Fillon et Mélenchon est représenté visuellement par un écart 3 fois plus important que celui qui est utilisé pour représenter les 5 % qui séparent Mélenchon de Hamon.
➜ Un écart en pourcentage deux fois plus faible est représenté par un écart visuel 3 fois plus grand !
(NB : l'annotation était déjà présente sur l'image).
Exemple : Données utilisées non conformes au titre du graphique
Plus difficile à détecter au premier abord, ce type de représentation graphique qui prétend vous permettre de visualiser une certaine chose, alors qu'elle est construite sur des données représentant une autre chose.
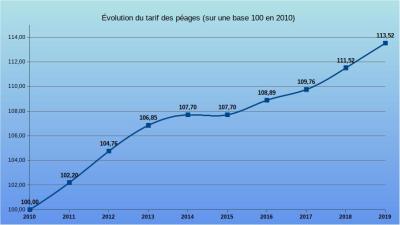
Par exemple, sur le graphique ci-dessous (journal Le Parisien – 18 janvier 2019), où les valeurs présentées sur le graphique ne représentant pas ce qui est annoncé par le titre.

Au premier coup d’œil, rien de spécial sur ce graphique qui nous permet de visualiser sur une courbe « l'évolution annuelle des prix des péages ».
Si on prend le temps de comprendre, on voit que cette courbe est construite avec des valeurs en pourcentage, qui ne représentent pas « l'évolution annuelle des prix » mais plutôt l'évolution annuelle des augmentations de prix.
➜ Ce n'est pas du tout la même chose !
Cette courbe trompeuse qui monte et qui descend laisse croire que parfois, selon les années, les prix augmentent et parfois ils diminuent. Or, il n'en est rien. Les valeurs affichées, qui, répétons-le, sont celles des augmentations de prix, montrent bien que les prix augmentent tous les ans et ne diminuent jamais.
Le type de représentation choisi est complètement trompeur.
Pour que chacun puisse appréhender la réalité des faits et se rende compte réellement de « l'évolution du prix des péages » comme c'était annoncé, il aurait bien mieux valu construire le graphique ci-contre, en prenant une année initiale de référence (l'année 2010, ici) associée à un indice 100 par exemple pour un prix initial, puis en en calculant les valeurs des prix de chaque année en tenant compte de l'augmentation.
On voit bien que ces deux graphiques ne donnent absolument pas la même impression, le même ressenti au lecteur.
Alors ? Simple erreur de choix ? Volonté délibérée de véhiculer un certain message, en accord avec l'opinion du journal qui l'a publié ?
Il est difficile, voire impossible de trancher, et c'est un autre débat…
Exemple : Erreur mathématique
Pas vraiment un graphique ici mais une présentation visuelle fausse à partir de données chiffrées, avec cette image issue du JT de 13h de France 2 du 19 février 2013, à propos de l'augmentation des tarifs de l’électricité :
Le présentateur (qui est tout de même éditorialiste économique à France 2) annonce une augmentation du prix de l'électricité de 6% par an pendant 5 ans et il se hasarde même à dire : « pas besoin d'avoir fait Polytechnique pour s'apercevoir que ça représente une hausse de 30 % »… !
On se rend donc compte que :
le journaliste n'a sans doute pas fait Polytechnique lui non plus,
il commet une erreur mathématique grossière en faisant le calcul : +6 % par an pendant 5 ans = 30 % d'augmentation.
➜ une augmentation de 6 % en un an correspond à un prix multiplié par 1,06.
La 2e année, le prix de la 1ère année sera encore multiplié par 1,06 et ainsi de suite.
Au bout de 5 ans, le prix initial sera multiplié par 1,065 = 1,338 soit une augmentation de 33,8 % (en non pas 30 %).
À voir sur l'extrait ci-dessous :
Exemple : Axe des ordonnées qui ne commence pas à zéro
Un grand classique pour la manipulation de graphiques : tronquer l'axe des ordonnées qui ne commencera donc pas à 0. À partir de là, on peut faire dire à peu près ce qu'on veut à ce genre de graphiques… Voir plus haut l'exemple à propos de la grève à la SNCF.
Sur cette image, deux choses :
en haut, le graphique tel qu'il a été diffusé sur France 2 : un graphique tronqué, sans aucune échelle de valeur en ordonnée (et où il est évident que si elle était visible, cette échelle ne commencerait pas à 0) ➜ la chute (bien réelle) de la côte de popularité de Mélenchon à ce moment-là est visuellement accentuée avec un aspect « dégringolade ».
en bas, le graphique tel qu'il aurait dû être présenté pour être rigoureux : l'axe des ordonnées a des graduations qui commencent à 0, on peut donc valablement comparer les valeurs ➜ la chute de la côte de popularité est évidemment toujours visible mais l'impression donnée est qu'elle paraît bien moins spectaculaire avec des valeurs comparables sur une même base.
NB : ce n'est pas une règle immuable que de devoir faire commencer l'axe des ordonnées à zéro, dans certains cas elle ne se justifie pas, mais ce qui est certain, c'est que c'est une pratique qui est invariablement « oubliée » par tous ceux qui veulent manipuler l'opinion avec des graphiques.
Ressources associées⚓
Dataviz ?
La « Data visualization » (souvent raccourcie en Dataviz) ou « Représentation graphique de données » est une science et un métier à part entière :
https://fr.wikipedia.org/wiki/Repr%C3%A9sentation_graphique_de_donn%C3%A9es
Complément : Trafic de graphiques
En complément, une vidéo qui reprend l'essentiel au sujet des graphiques erronés :
Complément : (Se) Tromper avec les graphiques
« Cette activité de lycée a pour but d'étudier différentes manières permettant de tromper (volontairement ou non) avec des graphiques. En d'autres termes, comment la représentation de vraies données statistiques permet de donner une impression erronée ? »
Vous trouverez ici une séance complète pour une classe de lycée, en rapport avec cette thématique, avec tous les documents associés disponibles au téléchargement. L'ensemble est publié sous licence libre CC-BY-SA.
Complément : Autres fiches pratiques
Recommandations d'usage et juridiques⚓
Pas de recommandation particulière sur les droits d'usage.